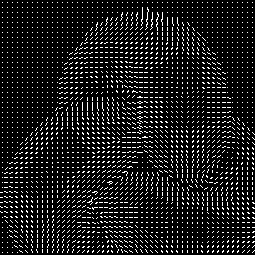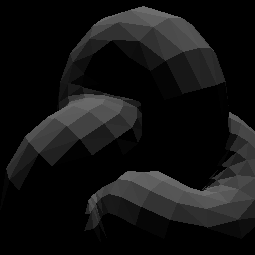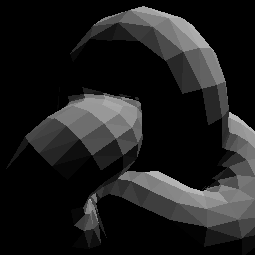This assignement shows the power of Photo Metric Stereo (PMS). The idea behind PMS extends that of Shape from Shading (SFS) based 3D reconstruction. With PMS the recovery of surfaces is based on their photometric properties (different irridiance values at one point for different illuminations) whereas the former methods use geometric models to reconstruct the surfaces. Because of the larger amount of data to be processed an improvement of the reconstruction results and a further reduction of necassary assumptions can be expected.
We use three images from the same scene under different illumination. Why two images are not enough can be read under Answers.
Assumptions
In static stereo analysis the scene is observed from different positions where pose and orientation of object and illumindation remain unchanged. In contrast PMS keeps the scene static, but the object is consecutively illumindated by several lightsources with constant radiance. Each images is taken with only one light source switched on and the camera modeling uses parallel projection. The camera is properly adjusted using calibration. The surfaces are ideal Lambertian reflectors (but the albedo is not necessarily constant) and the irradiances at a certain pixel are measurable. Movement in the system of objects, the lights and the camera does not occur. Thus we don't need to handle a may-be correspondence problem.Implementation (of the basic PMS algorithm)
We have implemented our program to be run in a batch environment, so without interaction with the user. All parameters are given through the commandline:
./ass4psm 3*[inputfile] 3*[ps-value] 3*[pq-value]In pseudo-code the algorithm looks like this (p, q and r initilized as given in the assignment's description, variable names according to the description):
beginThe algorithm uses images taken with three differently positioned light sources. The intersection(p,q) in gradient space represents the desired orientation. When the irradiances are measured for a real surface point, then possiblly there never exists a unique intersection due to noise and other errors. Thus our assumption is that there is a unique intersection point.compute the normal n for each point()end.
E1 = E01.albedo.(n.s1)/(||n||.||s1||)
E2 = E02.albedo.(n.s2)/(||n||.||s2||)
E3 = E03.albedo.(n.s3)/(||n||.||s3||)
p.ps1+q.qs1+1 ||s1|| E1 E02 ||s1|| E1 E02
------------- = ------.--.--- <=> ------.--.---- = r1
p.ps2+q.qs2+1 ||s2|| E2 E01 ||s2|| E2 E01
p.ps1+q.qs1+1 ||s3|| E1 E03 ||s3|| E1 E03
------------- = ------.--.--- <=> ------.--.---- = r2
p.ps3+q.qs3+1 ||s1|| E3 E01 ||s1|| E3 E01
E01/E02 = EMax1/EMax2 and E01/E03 = EMax1/EMax3
p.ps1+q.qs1+1 = r1.(p.ps2+q.qs2+1)
p.ps1+q.qs1+1 = r2.(p.ps3+q.qs3+1)
generate the needle map()
reconstruction()
After the calcullation of the gradients the viewer should obtain an impression of the 3D shape. Thus a reconstruction process is done with changing light position to get different illumination pictures for the object. The surface gradients are used to render the object by using the Lambertian reflection model with an arbitrary initial value for the illumination direction.
From our assumption we get: Light source is in infinite distance (parallel light beams) and its strength doesn't vary. The illumination directions are parallel through all surface points. The reflected surface is Lambertian reflection (now with constant albedo). So we have
E = E0.ñ.(n . l)wheren.l = (p.ps+q.qs+1)/((sqrt(p*p+q*q+1).sqrt(ps*ps+qs*qs+1)).Because ñ and n.l are known and E0 arbitrarily set (we set it to the maximum), we can calculate the image intensity for the light source. As the window handling with Halcon is not that fast, we had to add a pause before being able to write to the canvas. Otherwise there would be some points in the upper left part missing (as it is there where the first points are drawn).
Representation
A needle map is used to represent the gradients. Not every point is drawn with its correspondent representation of the gradients (basically a line), but only some of them. Those are regularly chosen from the original dataset by applying a grid an the image. The grid width is 5 pixel because with fewer data samples the representation wouldn't clearly visible (a loss of information). On the other hand it has shown from testing that too many gradients represented in the image only confuse the viewer and hide information.
Using the PSM algorithm we reconstructed the gradient maps. Those are shown here together with images of the reconstructed object surfaces as described before. Three examples are shown here, two of synthetic object and one of a real one. The method worked fine for these images, because they were almost free of noise and the light positions when taking the fotos were tracked and could be given exactly.
The parameters for the first reconstructed image were (p=0.0,q=0.5), for the second (p=0.5,q=1.0) and for the third (p=0.5,q=-1.0) with an assumed basic radiance of E0=255.
needle map reconstructed
This assignment shows how to derive a reconstruction of the original surface in 3D from given 2D images under different illuminations. The result of the algorithm heavily depends on the input data (i.e. noisy images) and how exact the position of the lights is given. The more clear the input data, the better the result of the 3D reconstruction. The images must not have to big hightlights as then, the original values of the pixels can't be restored and the approach PSM takes will fail (as it's based on that single pixel values). In small hightlights the original irridiance values could be reconstructed using elaborated interpolation techniques with the neighboring pixels. The best is if the scene had no highlights at all. This would correspond to the Lambertian reflection model we use here - all surfaces are perfectly diffuse.
Source for Photometric Stereo